Стабiлiзацiя деякого класу нелiнiйних систем, некерованих за першим наближенням

V.I. Korobov; M.O. Bebiya

doi:10.15407/dopovidi2014.02.020

Stabilization of some class of nonlinear systems that are uncontrollable the first approximation

Authors

V.I. Korobov
M.O. Bebiya

DOI:

https://doi.org/10.15407/dopovidi2014.02.020

Keywords:

nonlinear systems, stabilization, uncontrol

Abstract

The problem of stabilization for systems of the form x˙1=u,

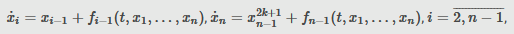
that are uncontrollable in the first approximation is considered. The sufficient condition of existence of a quadratic Lyapunov function is obtained, and a method of construction of the Lyapunov function and the stabilizing control is described.

Downloads

Download data is not yet available.

References

Korobov V. I. Method of control function. Moscow; Izhevsk: NITs “Reguliatornaia i khaoticheskaia dinamika”, 2007 (in Russian).

Savchenko A. Ya., Ignatev A. O. Some stability problems for nonautonomous dynamical systems. Kyiv: Nauk. dumka, 1989 (in Russian).

Kawski M. Syst. Control. Lett., 1989, 12: 169–175. https://doi.org/10.1016/0167-6911(89)90010-8

Cheng D., Lin W. IEEE Trans. Autom. Control., 2003, 48: 1242–1248. https://doi.org/10.1109/TAC.2003.814270

Hong Y., Wang J. Sci. China. Ser. F, 2006, 49, No. 1: 80–89. https://doi.org/10.1007/s11432-004-5114-1

Long L., Zhao J. Int. J. Contr., 2011, 84, No. 10: 1612–1626. https://doi.org/10.1080/00207179.2011.622790

Liao D. J. Theor. and Appl. Inform. Technol., 2012, 46, No. 1: 371–376.

Gao F., Li P., Yuan F. J. Inform. and Comput. Sci., 2013, 10, No. 4: 1139–1147. https://doi.org/10.12733/jics20101443

Downloads

PDF (Українська)

Published

27.03.2025

How to Cite

Korobov, V., & Bebiya, M. (2025). Stabilization of some class of nonlinear systems that are uncontrollable the first approximation . Reports of the National Academy of Sciences of Ukraine, (2), 20–25. https://doi.org/10.15407/dopovidi2014.02.020